Les Lois de Kepler
Johannes Kepler Kepler (1571-1630) naquit dans le Württemberg et suivit des études de théologie à Tübingen. Il adhéra très tôt au système de Copernic. Mathématicien brillant, il se vit offrir en 1594 à Graz un poste de professeur de mathématiques et d'astronomie : une partie de son travail consistait à préparer des almanachs, fournissant des données astronomiques et astrologiques. Le pouvoir grandissant de l'église catholique le contraignit, parce qu'il était protestant, à quitter Graz. C'est alors qu'il se réfugia à Prague, où il rencontra Tycho Brahé dont il devint l'assistant. Tycho demanda à Kepler de travailler à établir une théorie satisfaisante du mouvement des planètes, qui soit compatible avec la longue série d'observations qu'il avait effectuées à Hveen. A la mort de Tycho, il lui succéda comme mathématicien de l'empereur Rodolphe, et entra en possession de la plupart de ses observations il passa alors 25 ans de son existence à les interpréter. Son étude la plus détaillée porte sur la planète Mars, pour laquelle Tycho avait rassemblé une très grande quantité d'observations. Il publia ses premiers résultats en 1609 : il avait passé près de dix ans à essayer sans succès diverses combinaisons de mouvements circulaires, incluant des excentriques et des points équants : sa meilleure solution n'était en accord avec les observations qu'à la précision de 8', soit le quart du diamètre apparent de la Pleine Lune Kepler refusa d'admettre que Tycho ait pût faire cette erreur d'observation, même si petite, et il rejeta le modèle. Il chercha alors à représenter l'orbite de Mars par un ovale et découvrit que les observations étaient très bien représentées par une ellipse. |
 |
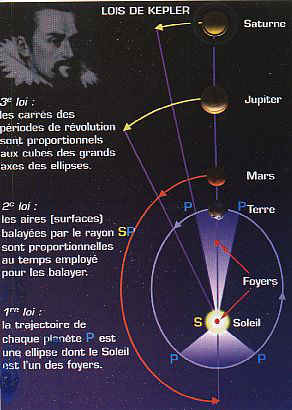 |
Les lois de Kepler Ces lois sont formulées de la façon suivante, dans un repère lié aux étoiles: Première loi (1605) : Chaque planète décrit autour du Soleil une orbite elliptique : le Soleil occupe l'un des foyers de l'ellipse. Deuxième loi (ou loi des aires) (1602) : Le rayon vecteur qui joint la planète au Soleil balaye des aires égales en des durées égales, quelles que soient ces durées . Troisième loi (1618) : Si a est le demi grand axe de t'orbite de la planète par rapport au Soleil et T sa période, a3/T2 est une constante pour l'ensemble des planètes du système solaire. C'est Newton qui donnera en 1687 l'explication des lois de Kepler, à partir de la loi de la gravitation Les mouvements des planètes. Les planètes sont toutes animées, comme la Terre, d'un mouvement de rotation propre et d'un mouvement de révolution autour du Soleil. Toutes les planètes décrivent leurs orbites dans le même sens, et les plans de ces orbites sont très voisins les uns des autres. La période du mouvement orbital de la planète, ou période sidérale, croît avec la distance de la planète au Soleil, depuis 88 jours pour Mercure, jusqu'à 248 ans pour Pluton. La composition du mouvement orbital de la planète avec celui de la Terre provoque le mouvement tel qu'on l'observe depuis la Terre, qui s'effectue avec une période différente, appelée période synodique. |
Résumé des propriétés d'une ellipse:
Une ellipse (Fig.) est caractérisée par ses deux foyers F et F' : tout point M de l'ellipse satisfait à la condition MF + MF' = 2a, où 2a est une constante, égale en particulier au plus grand diamètre de l'ellipse, qu'on appelle son grand axe. La distance du centre Q de l'ellipse à l'un ou l'autre des foyers est notée c : 0F = 0F' = c, et le rapport c/a est noté e et appelé excentricité. Enfin, le diamètre de l'ellipse perpendiculaire à son grand axe est appelé petit axe et noté 2b. On montre que a, b et c satisfont à la relation :
a2 = b2 + c2 = b2 + a2 x e2
Kepler montra que l'orbite de Mars est une ellipse dont l'excentricité est égale à 0,1 (elle vaut exactement 0,093). Tracée à l'échelle, l'orbite diffère très peu d'un cercle. Il a fallu la qualité des observations de Tycho Brahé et l'obstination de Kepler pour permettre d'établir qu'il s'agit d'une ellipse.
Avant d'établir que l'orbite de Mars est une ellipse, Kepler avait étudié la vitesse orbitale de la planète, et trouvé qu'elle est plus rapide quand Mars est plus proche du Soleil et plus lente quand Mars est plus loin. Il montra que les aires balayées pendant des intervalles de temps égaux, par le segment reliant Mars au Soleil, ont toujours la même valeur. Cette relation porte le nom de "loi des aires".
Il publia en 1609 "La Nouvelle Astronomie" qui étend à l'ensemble des planètes les résultats obtenus pour Mars, et établit et publia un peu plus tard, en 1619, dans "L'Harmonie des Mondes", la relation entre les grands axes des orbites et les périodes de révolution.